
📗第9回 乗算について学ぼう
皆さま、こんにちは!自宅CAN.COMの管理人のジタッピーです。第9回目となる今回は乗算について学んでいきますが、乗算は簡単にいうと掛け算のことです。
なお、検定ではパーセント(割合)の計算も必須となり、ラウンドセレクターや小数点セレクターを使用する端数処理も出てくるため、若干難しいと感じるかもしれません。ただ、ここを理解できるようになれば、第11回で説明する除算も基本的な考え方は同じなのですんなりと入り込めると思います。
今回は当講座の中でも最大の山場といっても過言ではなく、しっかりと読み込みながら進めていくのであれば、おそらく1時間以上は掛かると思うので、途中で休憩も取り入れつつ、乗り越えましょう!

あと、今回は初めて登場する聞きなれない単語が出てくるため、予め以下に記しておきます。
[無名数]単位がついていない数字のことを指す。 ※例)321
[名数]単位がついた数字のことを指す。 ※例)¥321
[端数処理]例えば小数点が出た際に四捨五入をするのか、切り捨てるのかといった処理をいう。
[帯小数]1以上の小数を指す。 ※例)4.321
[小数]整数の部分が0の小数を指す。 ※例)0.321
📖乗算の概要
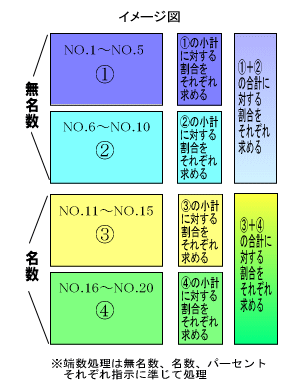
まず、乗算とは前述の通り、掛け算のことですが、検定においては無名数(NO.1~10)の計算、名数(NO.11~20)の計算、それぞれの小計、合計に対する個々の割合を求めるパーセントの計算があります。
また、全ての計算において、端数処理が必要な時には、ラウンドセレクター、小数点セレクターを使用して計算していきます。この端数処理の方法に関しては、問題用紙の上部に「(注意)」として、無名数、名数、パーセントそれぞれの処理についての方法が記されているので、それに準じて処理をしていきます。なお、言葉だけでは伝わりにくい部分もあるため、下記に図も作成しましたのでそちらも合わせてご覧ください。
出典:JPN-WORLD.COM
https://jpn-world.com/sikaku/sikakuouenhen/dentaku8.html
あとは、級によって桁数やパーセント以外の端数処理の問題数が異なっており、上級になれば桁数も増えていきます。ちなみにパーセント以外の端数処理の主題数は、3級では2題(無名数1題、名数1題)、2級では4題(無名数2題、名数2題)、1級では8題(無名数4題、名数4題)となっています。
乗算の概要は以上となります。それではここから全体のベースとなる端数処理の方法から説明していきます。
📖端数処理の方法
端数処理の方法は前述の通り、問題の上部に「(注意)」として記載されていますが、ざっくり言うと、これは小数点セレクター、ラウンドセレクターをどのように設定するかということになります。では、その「(注意)」の文を実際に見てみましょう。
| (注意) 無名数で小数第3位未満の端数が出たとき、名数で円位未満の端数が出たとき、パーセントの小数第2位未満の端数が出たときは四捨五入すること |
※第36回電卓計算能力検定試験3級乗算より引用
おそらく何の説明を受けたこともない方が、初めてこの文をみてもすぐに理解することは難しいかと思われますが、三つの文に分解すると理解しやすいと思います。
・無名数で小数第3位未満の端数が出たときは四捨五入すること
・名数で円位未満が出たときは四捨五入すること
・パーセントの小数第2位未満の端数が出たときは四捨五入すること
いかがでしょうか。実際にここからは数字を当てはめながら、それぞれ説明していきたいと思います。
■無名数の場合(小数第3位未満の端数が出たときは四捨五入)・・・例 3.18769
さっそくここで問題ですが、3.18769の小数第3位未満は、どの部分になるでしょうか。おそらく、小学生であれば普段学校で接しているので即答できるかと思いますが、普段、小数と関わりののない方々は、年齢を重ねていくにつれて「小数の未満ってどうなるんだったかな?」というようになってしまうのではないかと思います。ちなみに正解は187までが小数第3位であるため、小数第3位未満は69となります。
では、次にこの69の部分を四捨五入することが求められているので、そのまま四捨五入します。そうすると3.188となり、これが正解となります。今は電卓は使用せずに暗算で四捨五入をしましたが、電卓ではセレクターの機能にて、自動で四捨五入するように設定します。
設定方法はまず、ラウンドセレクターを四捨五入を行う「5/4」に合わせます。続いて小数点以下第3位まで表示させる必要があるため、小数点セレクターを「3」に設定します。あとはこの状態で計算をすれば、常に小数第3位未満は四捨五入して表示されます。もし、セレクターの使い方を忘れてしまったという方は、「第3回 電卓の機能を知ろう」を今一度見直してみましょう。
■名数の場合(円位未満の端数が出たときは四捨五入)・・・例 ¥83.3
次に名数の場合についてですが、名数の場合には円位未満が出たときは四捨五入とあります。そもそも円位未満とは何なのかを理解する必要がありますが、円の最小の単位は1円なので、1円未満は小数のこととなります。つまり、小数が出た場合には四捨五入するということになるので、小数が答えになるということはありません。今回の例では¥83が正解になりますが、これを電卓で設定すると、小数は表示させないので小数点セレクターは「0」、ラウンドセレクターは「5/4」となります。
■パーセントの場合(小数第2位未満の端数が出たときは四捨五入)・・・例 68.5472%
最後にパーセントの場合ですが、小数第2位未満を四捨五入とあるので、今回の例では72の部分を四捨五入します。そうすると68.55%となりますが、これを電卓のセレクターでは、ラウンドセレクターは「5/4」、小数点セレクターは「2」に合わせて計算します。最初に見た無名数の場合と小数の位が違うだけなので、難しくないかと思います。
端数処理の方法はこれで以上となりますが、あまりよく理解ができなかったという方は、とりあえず「無名数の時はこれとこれ、名数の時はこれとこれを設定する」というように機械的に覚えるのも一つの方法かと思います。
さて、次は無名数の計算、名数の計算、パーセントの計算について説明していきますが、ここからは説明が長くなるので、一度この辺で休憩することをおススメします。
📖無名数の計算(NO.1~NO.10)について
まず、無名数の計算には、NO.1~NO.5(整数×整数)とNO.6~NO.10(小数or帯小数×小数or帯小数)の2つのグループが存在し、それぞれのグループごとに小計を計算していきます。次にそれぞれのグループの小計を合計し、最後はそれらの結果をベースに、後に説明するパーセントを計算していきます。
このように全てが連係している為、1題でも誤って計算をしてしまうと、パーセントの計算にも大きく響いてくるので、確実に計算していく事が求められます。
なお、端数処理はNO.1~NO.5において発生はせず、どの級(レベル)でもNO.6~NO.10の中で発生するので、計算する直前にラウンドセレクターを「5/4」、小数点セレクターを「3」に設定してから計算するということを抑えておきましょう。
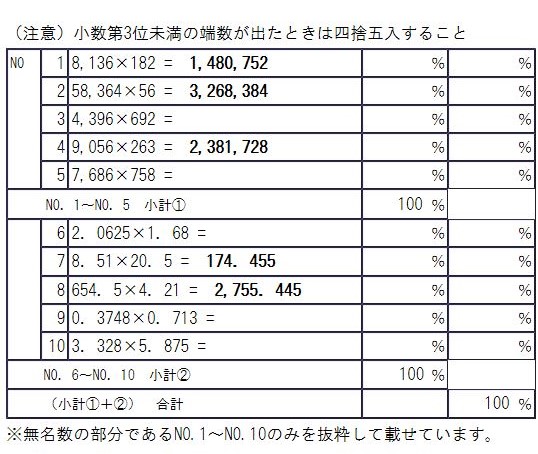
では、以上のことを踏まえて、まずは下記の空欄になっている部分を実際に計算してみましょう。パーセントについては後に計算するため、そこは除き、小計と合計まで計算しましょう。
【練習問題】(制限時間2分)
出典:JPN-WORLD.COM
https://jpn-world.com/sikaku/sikakuouenhen/dentaku9.html
いかがでしたでしょうか。NO.1~NO.5に関しては、端数処理もなく、そのまま単純に計算するだけなので簡単かと思いますが、NO.3の答えは3,042,032、NO.5は5,825,988となります。
続いてNO.6~NO.10ですが、この中には端数処理の問題が含まれています。なお、全経の出題範囲の中にも、どの部分が端数処理になるのかが記載されており、3級では小数×小数で1題出題されるとあります。一応、上記の練習問題であれば、NO.9がそれに該当します。ただ、実際には予めセレクターを設定して計算すると、常に端数が出ても小数第3位までしか表示されないため、どれが端数処理の問題なのかは分かりません。従って、そこは全く気にせずに計算するようにしましょう。ちなみに1級レベルにまでなると、5問中4問が端数処理という構成になっているので、気にするだけ時間の無駄になります。
さて、この練習問題の解答についてですが、NO.6は3.465、NO.9は0.267、NO.10は19.552となります。
あと、小計と合計はそのまま足すだけで、小計①はNO.1~5の結果を全て足して15,998,884となり、小計②はNO.6からNO.10の結果を全て足して2,953.184が正解となります。合計は小計①+②なので16,001,837.184となります。
では、次に名数の計算です。
📖名数の計算(NO.11~NO.20)について
名数の計算も無名数と同じようにNO.11~NO.15(名数×整数)、NO.16~NO.20(名数×小数or帯小数)という2つのグループに分かれていますが、計算がされていない部分をそれぞれ計算していき、グループごとの小計も計算し、さらにそれぞれの小計を合わせて、名数としての合計まで計算します。そして、この結果をもとに、パーセントも計算をしていきます。
なお、端数処理は、どの級(レベル)においても、NO.16~NO.20にて発生するため、計算する直前に必ずラウンドセレクターを「5/4」、小数点セレクターを「0」に設定をしてから計算しましょう。言い換えると、NO.11~NO.15の中では端数処理は発生しないということになります。
基本的には無名数と似たような感じではありますが、名数では解答する際に¥が必要となるので、その点には気を付けましょう。
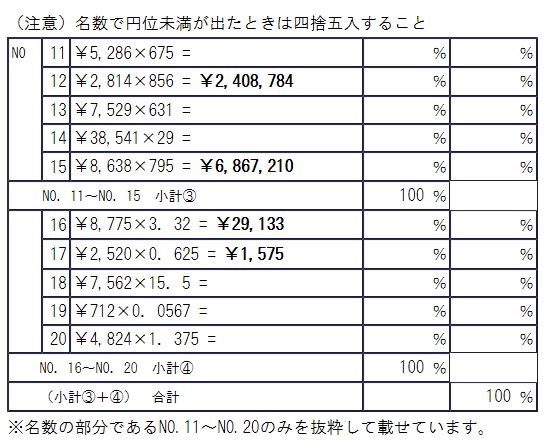
それでは、以上のことを踏まえ、下記の練習問題で空欄になっている部分を計算し、小計と合計まで計算してみましょう。なお、パーセントは後ほど計算するので、空欄で構いません。
【練習問題】(制限時間2分)
出典:JPN-WORLD.COM
https://jpn-world.com/sikaku/sikakuouenhen/dentaku9.html
いかがでしたでしょうか。それでは答え合わせをしていきしょう。まず、NO.11~NO.15に関してはそのまま計算するだけでとなりますが、NO.11は¥3,568,050、NO.13は¥4,750,799、NO.14は¥1,117,689が正解です。
次にNO.16~NO.20ですが、この中には端数処理の問題が含まれています。ただ、無名数と同じようにどの問題が端数処理なのかは気にする必要はありません。解答はNO.18が¥117,211、NO.19が¥40、NO.20が¥6,633になります。
小計と合計については、無名数の時と同じようにそのまま足すだけです。小計③はNO.11~15の結果を全て加算すると¥18,712,532、小計④もNO.16からNO.20の結果を全て加算すると¥154,592となります。合計は小計③+④なので¥18,867,124が正解となります。
では、続いてパーセントの計算です。
📖パーセントの計算について
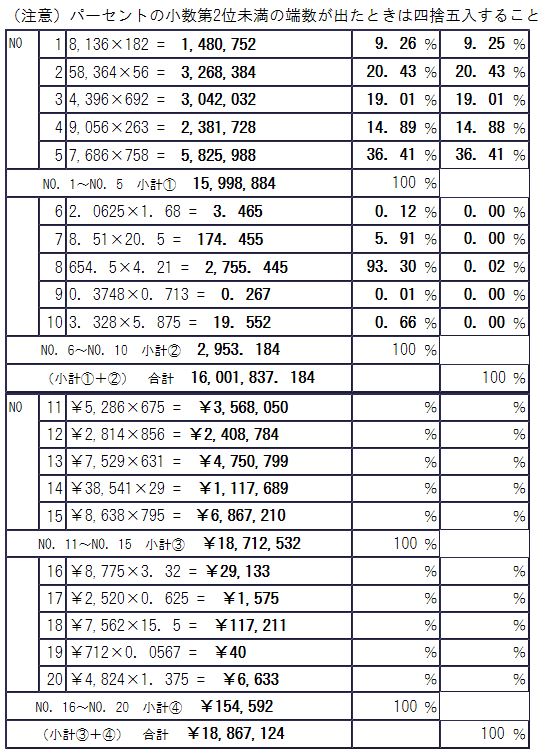
さて、ここからは乗算の最後となるパーセントの計算についてみていきますが、解答欄をご覧の通り、パーセントの欄が2列あります。これは左側の列が小計①~④に対するそれぞれの割合、一方の右側列は、無名数、名数に対するそれぞれの割合となっています。
なお、ここでは、ほとんどの計算において端数処理が発生するため、予めセレクターを小数第2位未満を四捨五入して、小数点以下第2位まで表示させるように、ラウンドセレクターを「5/4」、小数点セレクターは「2」に設定します。
ただ、パーセントの計算においては、解答する際に注意しなければならない点が一つあります。それは答えが0や9といった整数の場合、あるいは1.1のように小数第1位で終わる場合でも、0.00、9.00、1.10といったように、小数第2位まで書かないと不正解となってしまうため、注意しましょう。
【左側の列のパーセントの計算方法】
それではまず、割合を求める計算式についてですが、割合=個÷全体×100という式になります。電卓検定であるからといって特別に何かが異なるということはありません。では次に、実際に式を当てはめながらみてみましょう。
NO.1の場合は、個が1,480.752、全体が小計①の15,998,884となるため、式にすると以下のようになります。
割合=1,480.752÷15,998,884×100
なお、NO.1の解答は四捨五入されるため、9.26となります。NO.2~NO.5についても同様に計算していきます。このことからも分かるように、小計①はNO.2~NO.5でも使用することになるので、効率よく計算していくためにも、「M+」を押して、電卓に記憶させ、計算を繰り返すようにしましょう。
続いてNO.6~NO.10も同様です。全体となる小計②をベースに「割合=個(NO.6~NO.10)÷全体(小計②)×100」という計算式で、それぞれ計算をしていきます。
おそらく慣れてくると、最後に100を掛け算すること自体が面倒になってきます。その場合は、予め個を暗算で100倍した状態にして、計算することも可能であり、そのほうが時間は短縮できます。
【例】
NO.1の場合:割合=148,075,200÷小計①
NO.9の場合:2.67÷小計②
ただ、単純に100を掛けるだけとはいえ、もちろん計算ミスをしてしまう可能性もあるので、慣れない最初のうちは、計算式通り、無難に計算した方がよいのかもしれません。
【右側の欄のパーセントの計算方法】
続いて、右側の欄のパーセントの計算方法ですが、極めて単純です。ここでは小計①+小計②の無名数の合計に対してのNO.1~NO.10の割合を求める計算になります。そのため、式では「割合=個(NO.1~NO.10)÷全体(合計)×100」となり、この式に当てはめ、NO.1~NO.10まで、それぞれ計算していくだけとなります。
それでは、これらを踏まえた上で下記の練習問題にチャレンジしてみましょう。
【練習問題】(制限時間2分)
下記の空欄になっている名数のパーセントをそれぞれ計算しましょう。
出典:JPN-WORLD.COM
https://jpn-world.com/sikaku/sikakuouenhen/dentaku9.html
さて、いかがでしたでしょうか。さっそく解答ですが、下記の通りになります。
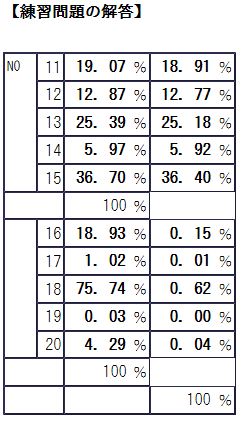
出典:JPN-WORLD.COM
https://jpn-world.com/sikaku/sikakuouenhen/dentaku9.html
それでは、以上でパーセントの計算については終了です。次は計算する順序及び採点箇所について説明していきます。
📖採点及び計算する順序について
ここでは採点及び計算する順序について説明をしていきます。
まず、採点については、乗算は見取算とは異なり、全てが採点の対象になるということではなく、ランダムに25箇所設定されています。得点の配分に関しては、パーセント以外の無名数と名数の計算が6割、左側の列のパーセントが2割、そして右側の列のパーセントが2割となっています。
ちなみに1級から3級は、7割以上で合格となるので、そのレベルを目指す場合は、今回説明した順序(パーセント以外の無名数・名数の計算 → 左側の列のパーセントの計算 → 右側の列のパーセントの計算)で計算した方が、時間が足りなくなった場合でも、左側の列のパーセントの計算まで終わってさえいれば、8割は到達できます。
ただ計算の順序は、例えばNO.1~NO.5の小計を出し、すぐにその時点でM+を押して、即パーセントの計算に入るなど様々あります。そのため、どの方法が早く、また自分に合うのかなど、様々なパターンで計測し、色々試してみるのもよいかと思います。もし、段レベルの実力者が周辺にいる場合には、どのような方法で計算しているのかなど、参考程度に聞いてみるのもありかと思います。
それでは以上で乗算は終了です。おそらく、電卓の乗算に触れたのが今回の講座が初めてだったという方であれば、内容が濃かった分、大変だったかと思います。ただ、ここをしっかりと理解すれば、第11回で説明する除算についても、すぐに理解することが可能なのでしっかりと復習し、理解を深めましょう。さて、次回は乗算の練習問題に取り組みます。
[記事公開日:2020年5月17日]




![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/04afba5f.045358f6.04afba60.21123643/?me_id=1213310&item_id=13830103&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6645%2F9784820746645.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6645%2F9784820746645.jpg%3F_ex%3D300x300&s=300x300&t=picttext)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1b01f4a6.726ac634.1b01f4a7.058844d5/?me_id=1285657&item_id=11806200&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbookfan%2Fcabinet%2F00774%2Fbk4820726277.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbookfan%2Fcabinet%2F00774%2Fbk4820726277.jpg%3F_ex%3D240x240&s=240x240&t=picttext)
